Tablas estadísticas

En el ámbito de la estadística, una parte importante son las funciones estadísticas, tanto continuas como discretas, que nos permiten determinar las probabilidades de un suceso, partiendo del modelo estadístico al que ese suceso se ajusta.

En la práctica, cuando queremos saber el valor numérico de esa probabilidad, no solamente la expresión que la determina, necesitamos cuantificar la distribución de probabilidad, que no suelen ser expresiones sencillas, en los últimos tiempos el desarrollo de la informática, facilita grandemente estos cálculos, pero la utilización de tablas estadísticas es lo más corriente.

Variables cualitativas

Son el tipo de variables que como su nombre lo indica expresan distintas cualidades, características o modalidad. Cada modalidad que se presenta se denomina atributo o categoría, y la medición consiste en una clasificación de dichos atributos. Las variables cualitativas pueden ser dicotómicas cuando sólo pueden tomar dos valores posibles, como sí y no, hombre y mujer o ser politómicas cuando pueden adquirir tres o más valores. Dentro de ellas podemos distinguir:

• Variable cualitativa ordinal o variable cuasicuantitativa: La variable puede tomar distintos valores ordenados siguiendo una escala establecida, aunque no es necesario que el intervalo entre mediciones sea uniforme, por ejemplo: leve, moderado, fuerte.

• Variable cualitativa nominal: En esta variable los valores no pueden ser sometidos a un criterio de orden, como por ejemplo los colores.

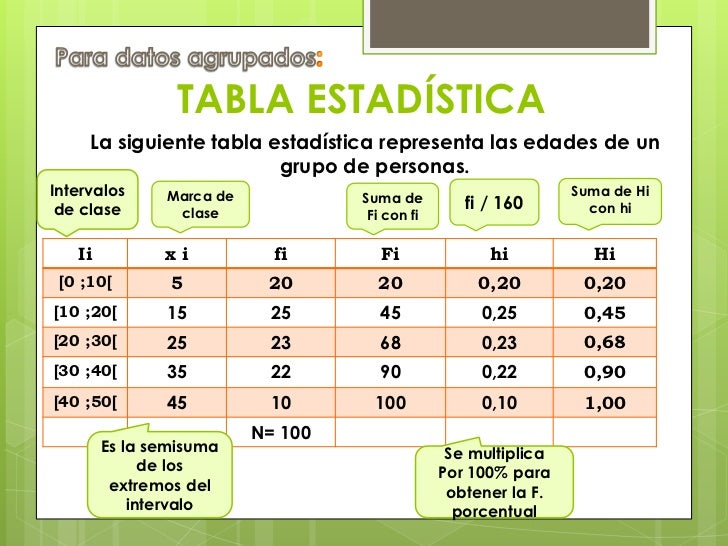
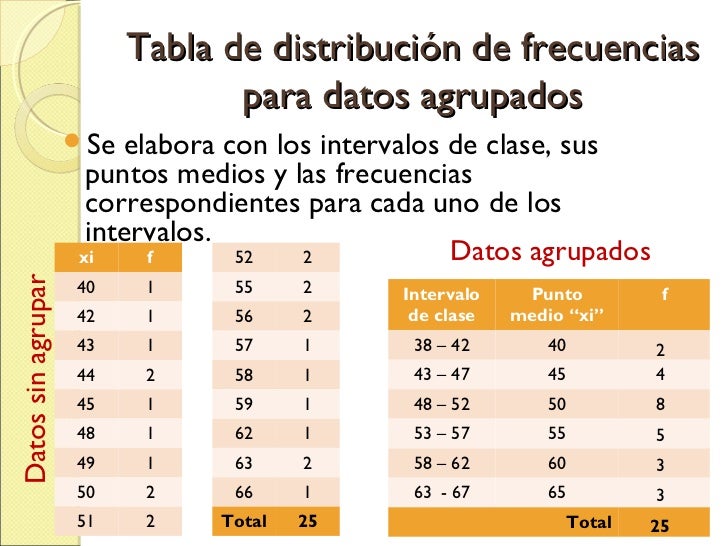
Tablas de frecuencias con datos agrupados

Cuando los valores de la variable son muchos, conviene agrupar los datos en intervalos o clases para así realizar un mejor análisis e interpretación de ellos.

Para construir una tabla de frecuencias con datos agrupados, conociendo los intervalos, se debe determinar la frecuencia absoluta (fi) correspondiente a cada intervalo, contando la cantidad de datos cuyo valor está entre los extremos del intervalo. Luego se calculan las frecuencias relativas y acumuladas, si es pertinente.

Si no se conocen los intervalos, se pueden determinar de la siguiente manera:

Se busca el valor máximo de la variable y el valor mínimo. Con estos datos se  determina el rango.

Se divide el rango en la cantidad de intervalos que se desea tener, obteniéndose así la amplitud o tamaño  de cada intervalo.

Comenzando por el mínimo valor de la variable, que será el extremo inferior del  primer intervalo, se suma a este valor la amplitud para obtener el extremo superior  y así sucesivamente.

                                          

Variables cuantitativas

Son las variables que toman como argumento cantidades numéricas, son variables matemáticas. Las variables cuantitativas además pueden ser:

• Variable discreta: Es la variable que presenta separaciones o interrupciones en la escala de valores que puede tomar. Estas separaciones o interrupciones indican la ausencia de valores entre los distintos valores específicos que la variable pueda asumir. Ejemplo: El número de hijos (1, 2, 3, 4, 5).

• Variable continua: Es la variable que puede adquirir cualquier valor dentro de un intervalo especificado de valores. Por ejemplo la masa (2,3 kg, 2,4 kg, 2,5 kg,...) o la altura (1,64 m, 1,65 m, 1,66 m,...), o el salario. Solamente se está limitado por la precisión del aparato medidor, en teoría permiten que exista un valor entre dos variables.

Gráficas para variables cuantitativas

Para las variables cuantitativas, consideraremos dos tipos de gráficos, en función de que para realizarlos se usen las frecuencias (absolutas o relativas) o las frecuencias acumuladas:

-Diagramas diferenciales:

Son aquellos en los que se representan frecuencias absolutas o relativas. En ellos se representa el número o porcentaje de elementos que presenta una modalidad dada.

-Diagramas integrales:

Son aquellos en los que se representan el número de elementos que presentan una modalidad inferior o igual a una dada. Se realizan a partir de las frecuencias acumuladas, lo que da lugar a gráficos crecientes, y es obvio que este tipo de gráficos no tiene sentido para variables cualitativas.

Según hemos visto existen dos tipos de variables cuantitativas: discretas y continuas. Vemos a continuación las diferentes representaciones gráficas que pueden realizarse para cada una de ellas así como los nombres específicos que reciben.

Gráficos para variables discretas

Cuando representamos una variable discreta, usamos el diagrama de barras cuando pretendemos hacer una gráfica diferencial. Las barras deben ser estrechas para representar el que los valores que toma la variable son discretos. El diagrama integral o acumulado tiene, por la naturaleza de la variable, forma de escalera. Un ejemplo de diagrama de barras así como su diagrama integral correspondiente están representados en la figura 1.6.

Ejemplo

Se lanzan tres monedas al aire en 8 ocasiones y se contabiliza el número de caras, X, obteniéndose los siguientes resultados: 

Representar gráficamente el resultado.

Solución: En primer lugar observamos que la variable X es cuantitativa discreta, presentando las modalidades:

Ordenamos a continuación los datos en una tabla estadística